Tensor Network Kalman Filter for Large-Scale MIMO Systems: With Application to Adaptive Optics

Abstract

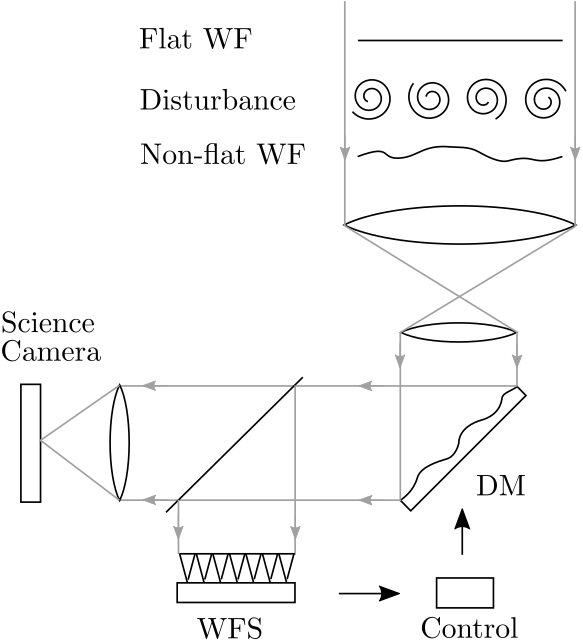
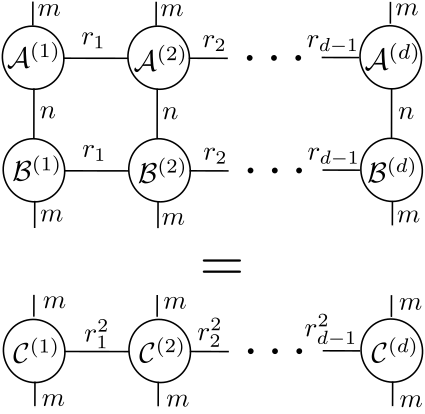
For large-scale system with tens of thousands of states and outputs the computation in the conventional Kalman filter becomes time-consuming such that Kalman filtering in large-scale real-time application is practically infeasible. A possible mathematical framework to lift the curse of dimensionality is to lift the problem in higher dimensions with the use of tensors and then decompose it. The tensor-train decomposition is chosen due to its computational advantages for systems with low tensor-train rank. Within this thesis two main limitations of the existing tensor Kalman filter are solved. First, a method is developed based on tensor-train rank truncation of the covariances to increase the computational speed for more general systems. Second, a MIMO tensor Kalman filter is developed for a specific class of systems. The power of the developed methods is shown on the example of adaptive optics which fits into the framework. A comparison with state-of-the-art large-scale estimation algorithms shows the computational advantage of the tensor Kalman filter at the cost of approximation errors.

This master thesis contains the publication Tensor Network Kalman Filter for LTI Systems.

Author: Daniel Gedon
Publication: Master Thesis, TU Delft
Links: Thesis Slides
BibTeX Citation:

@mastersthesis{gedon2019masterthesis,
    author={Daniel Gedon},
    title={Tensor Network Kalman Filter for Large-Scale MIMO Systems: With Application to Adaptive Optics},
    school={Delft University of Technology},
    address={the Netherlands},
    year={2019},
    }

Back to page: Publications or Talks.